Задание 4. Информатика. ЕГЭ. Шастин. 6.11.2024
- Просмотры: 2420
- Изменено: 2 февраля 2025
(Л. Шастин) По каналу связи передаются сообщения, содержащие только семь букв: А. М, Н, Е, З, И ,Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для букв известны: А — \(010\), М — \(000\), Н — \(100\), Е — \(101\), З — \(001\), И — \(011\), Я — \(1101\). Как можно сократить код для буквы Я таким образом, чтобы суммарная длина всех кодовых слов осталась прежней, а также сохранилось выполнение условия Фано? При этом допускается изменять коды, соответствующие остальным буквам. В качестве ответа укажите количество возможных (более коротких) кодовых слов для буквы Я.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение:
Первоначальное кодирование выглядит следующим образом.
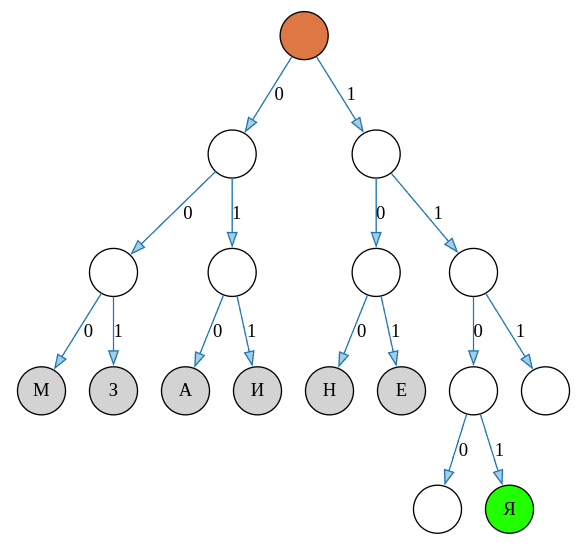
Суммарная длина кодовых слов в этом случае \(6 \cdot 3 + 4 = 22\). Очевидно, что букву Я можно переместить на уровень выше (на третий уровень), а одну из шести оставшихся букв — на четвёртый уровень. Суммарная длина кодовых слов не изменится. Один из возможных вариантов выглядит так.
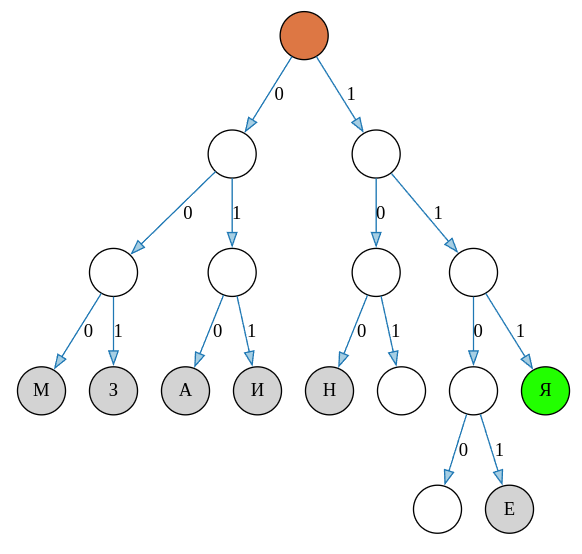
Всего на третьем уровне букву Я можно разместить восемью различными способами. Кроме того, эту букву можно поднять выше на второй уровень, тогда другую букву нужно будет опустить на пятый уровень. Например,
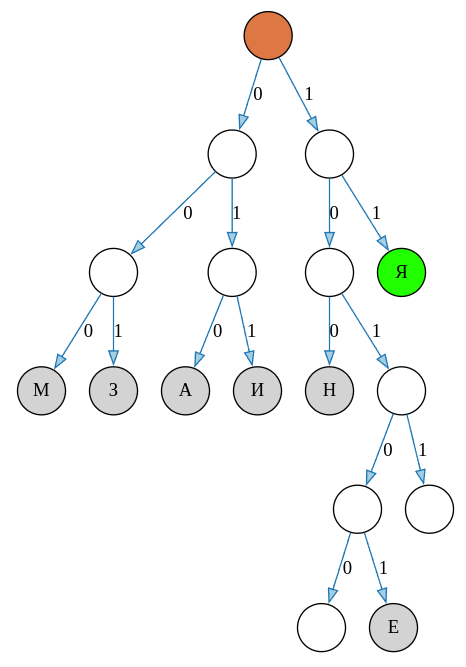
Всего существует \(4\) разных способа разместить букву Я на втором уровне. А вот на первый уровень отправить Я не получится не нарушив того условия, что суммарная длина кодовых слов останется неизменным. Таким образом, всего \(8 + 4 = 12\) вариантов.
Ответ: \(12\)