Задание 6. Информатика. ЕГЭ. Шастин. 18.10.2024
- Просмотры: 573
- Изменено: 31 января 2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 5 [Вперёд 15 Налево 90 Вперёд 25 Налево 90] Поднять хвост Вперёд 4 Налево 90 Вперёд 12 Налево 90 Опустить хвост Повтори 6 [Вперёд 38 Направо 90 Вперёд 22 Направо 90]
Определите периметр области пересечения фигур, ограниченных заданным алгоритмом линиями.
Решение:
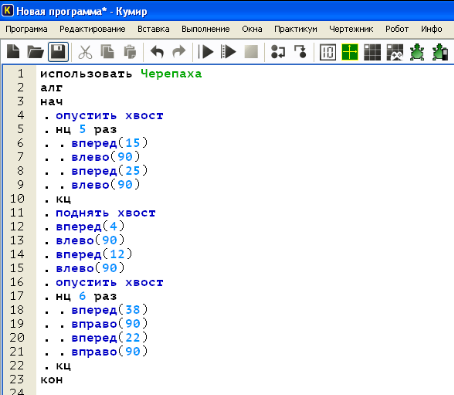
Запись алгоритма в среде Кумир
Результат выполнения — два пересекающихся прямоугольника:
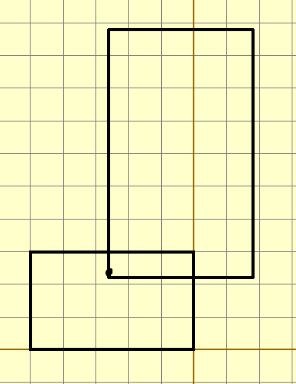
Координаты вершин первого прямоугольника: \((0, \, 0)\), \((0, \, 15)\), \((-25, \, 15)\), \((-25, \, 0)\). Координаты вершин второго прямоугольника: \((-13, \, 11)\), \((-13, \, 49)\), \((9, \, 49)\), \((9, \, 11)\). Длины сторон прямоугольника пересечения \(4\) и \(13\). Периметр \(P = 2 \cdot 4 + 2 \cdot 13 = 34\)
Ответ: \(34\)