Задание 6. Информатика. ЕГЭ. Шастин. 6.11.2024
- Просмотры: 1282
- Изменено: 1 февраля 2025
(Д. Бахтиев) Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, её голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует \(6\) команд: Поднять хвост, означающая переход к перемещению без рисования; Опустить хвост, означающая переход в режим рисования; Вперёд \(n\) (где \(n\) – целое число), вызывающая передвижение Черепахи на \(n\) единиц в том направлении, куда указывает её голова; Назад \(n\) (где \(n\) – целое число), вызывающая передвижение в противоположном голове направлении; Направо \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов по часовой стрелке, Налево \(m\) (где \(m\) – целое число), вызывающая изменение направления движения на \(m\) градусов против часовой стрелки. Запись
Повтори k [Команда1 Команда2 … КомандаS]означает, что последовательность из \(S\) команд повторится \(k\) раз. Черепахе был дан для исполнения следующий алгоритм:
Повтори 4 [Вперёд 16 Налево 90 Вперёд 20 Налево 90] Поднять хвост Вперёд 4 Налево 90 Вперёд 8 Направо 180 Опустить хвост Повтори 3 [Вперёд 35 Налево 90 Вперёд 6 Налево 90]
Определите периметр области объединения фигур, ограниченных заданным алгоритмом линиями.
Решение:
Нарисуем с помощью Python получившиеся фигуры
import turtle
t = turtle.Turtle()
t.speed(0)
t.goto(0, 0)
k = 10
t.down()
t.width(3)
t.left(90)
t.color('green')
for i in range(4):
t.forward(16 * k)
t.left(90)
t.forward(20 * k)
t.left(90)
t.up()
t.forward(4 * k)
t.left(90)
t.forward(8 * k)
t.right(180)
t.down()
t.color('red')
for i in range(3):
t.forward(35 * k)
t.left(90)
t.forward(6 * k)
t.left(90)
t.hideturtle()
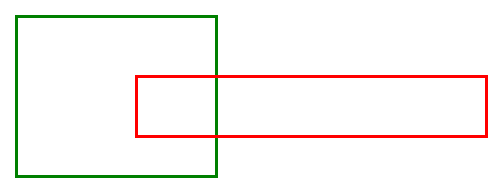
Зелёный прямоугольник имеет размеры \(16 \times 20\), красный — \(35 \times 6\). Причём красный выступает из зелёного прямоугольника на \(35 - 8 = 27\). Т.о., периметр фигуры, получившейся в результате объединения этих прямоугольников будет \(P = (16 + 20) \cdot 2 + 27 \cdot 2 = 126\).
Ответ: \(126\)