Задание 6. Информатика. ЕГЭ. Статград. 24.10.2024-1
- Просмотры: 1677
- Изменено: 1 февраля 2025
Исполнитель Черепаха передвигается по плоскости и оставляет след в виде линии. Черепаха может выполнять три команды: Вперёд \(n\) (\(n\) – число), Направо \(m\) (\(m\) – число) и Налево \(m\) (\(m\) – число). По команде Вперёд \(n\) Черепаха перемещается вперёд на \(n\) условных единиц. По команде Направо \(m\) Черепаха поворачивается на месте на \(m\) градусов по часовой стрелке, при этом соответственно меняется направление дальнейшего движения. По команде Налево \(m\) Черепаха поворачивается на месте на \(m\) градусов против часовой стрелки, при этом соответственно меняется направление дальнейшего движения. В начальный момент Черепаха находится в начале координат и направлена вверх (вдоль положительного направления оси ординат). Запись Повтори \(k\) [Команда1 Команда2 … КомандаS] означает, что заданная последовательность из \(S\) команд повторится \(k\) раз.
Черепаха выполнила следующую программу:
Повтори 2 [Вперёд 23 Направо 90 Вперёд 10 Направо 90] Вперёд 3 Налево 90 Вперёд 12 Направо 90 Повтори 2 [Вперёд 9 Направо 90 Вперёд 32 Направо 90]
Полученный при выполнении этой программы рисунок можно рассматривать как набор непересекающихся прямоугольников. Определите наибольшую из площадей этих прямоугольников. В ответе запишите только число – наибольшую площадь в условных единицах.
Решение:
В результате выполнения программы Черепаха нарисует следующие фигуры
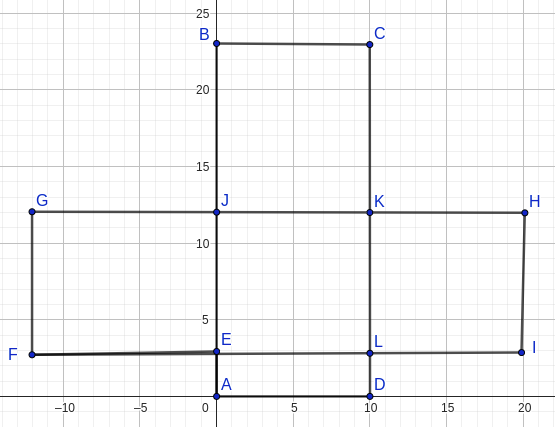
Нетрудно определить площади получившихся прямоугольников:
\(S_{AELD} = 3 \cdot 10 = 30\),
\(S_{EFGJ} = 12 \cdot 9 = 108\),
\(S_{EJKL} = 9 \cdot 10 = 90\),
\(S_{LKHI} = 9 \cdot 10 = 90\),
\(S_{JBCK} = 10 \cdot 11 = 110\).
Ответ: \(110\)