В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.

По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – прямоугольников размером \(3 \times 3\) так, что каждая точка попадает ровно в один кластер.

Центроидом кластера называется та из входящих в него точек, для которой минимальна сумма расстояний до всех остальных точек кластера. Обработка результатов эксперимента включает следующие шаги:

1. кластер, содержащий наибольшее число точек, исключается;
2. определяются центроиды всех оставшихся кластеров;
3. для найденных центроидов вычисляется средняя точка. Средней для группы точек называется точка (не обязательно входящая в группу), координаты которой определяются как средние арифметические значения координат всех точек группы.

В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить среднюю точку центроидов всех кластеров за исключением содержащего наибольшее число точек.

Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите координаты средней точки по описанным выше правилам. В ответе запишите четыре числа: сначала (в первой строке) координаты \(X\) и \(Y\) средней точки для файла A, затем (во второй строке) координаты \(X\) и \(Y\) средней точки для файла B. В качестве значения координаты указывайте целую часть от умножения числового значения координаты на \(10~000.\)

Файл с данными

В лаборатории проводится эксперимент, состоящий из множества испытаний. Результат каждого испытания представляется в виде пары чисел. Для визуализации результатов эта пара рассматривается как координаты точки на плоскости, и на чертеже отмечаются точки, соответствующие всем испытаниям.

По результатам эксперимента проводится кластеризация полученных результатов: на плоскости выделяется несколько кластеров – прямоугольников размером \(3 \times 3\) так, что каждая точка попадает ровно в один кластер.

Центроидом кластера называется та из входящих в него точек, для которой минимальна сумма расстояний до всех остальных точек кластера. Обработка результатов эксперимента включает следующие шаги:

1. кластер, содержащий наименьшее число точек, исключается;
2. определяются центроиды всех оставшихся кластеров;
3. для найденных центроидов вычисляется средняя точка. Средней для группы точек называется точка (не обязательно входящая в группу), координаты которой определяются как средние арифметические значения координат всех точек группы.

В файле записан протокол проведения эксперимента. Каждая строка файла содержит два числа: координаты \(X\) и \(Y\) точки, соответствующей одному испытанию. По данному протоколу надо определить среднюю точку центроидов всех кластеров за исключением содержащего наименьшее число точек.

Вам даны два входных файла (A и B), каждый из которых имеет описанную выше структуру. По данным каждого из представленных файлов определите координаты средней точки по описанным выше правилам. В ответе запишите четыре числа: сначала (в первой строке) координаты \(X\) и \(Y\) средней точки для файла A, затем (во второй строке) координаты \(X\) и \(Y\) средней точки для файла B. В качестве значения координаты указывайте целую часть от умножения числового значения координаты на \(10~000.\)

Файл с данными

(Д. Бахтиев) Учёный решил провести кластеризацию множества звёзд по их расположению на карте звёздного неба. Каждая звезда задаётся своими координатами \((x, \, y).\) Две звезды считаются соседними, если расстояние между ними по формуле Евклида $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ строго меньше \(1\) условной единицы.

При этом используется следующее определение кластера и аномалии: звезды принадлежат одному и тому же кластеру, если между ними существует цепочка соседних звёзд (то есть, для любой пары звёзд \(A\) и \(B\) в кластере можно найти последовательность $$ A = P_1, \, P_2, \, \ldots , P_k = B, $$ где расстояние между соседними звёздами \(P_i\) и \(P_{i+1}\) меньше \(1\)). При этом кластером считается только такое объединение звёзд, в котором общее число точек не менее \(20.\) Если какая-либо группа звёзд, связанная по вышеописанному принципу, содержит менее \(20\) точек, она не рассматривается как кластер, а все входящие в неё звёзды считаются аномалиями.

Входные данные задаются в двух файлах: файл \(A\) и файл \(B.\) В каждой строке файлов содержатся координаты звёзд: сначала по оси \(x,\) затем по оси \(y.\) При условии, что аномалии при расчётах игнорируются, требуется определить координаты центроида самого маленького (по числу звёзд) кластера. Центроид кластера определяется как звезда, принадлежащая кластеру, для которой сумма расстояний до всех остальных звёзд этого кластера минимальна. Гарантируется, что такой кластер определяется однозначно. В ответе запишите четыре числа: в первой строке для файла \(A\) результаты произведений \(C_x \cdot 10000\) и \(C_y \cdot 10000,\) где \(C_x\) и \(C_y\) — координаты центроида кластера по осям \(x\) и \(y\) соответственно, а во второй строке аналогичные данные для файла \(B.\)

Файл с данными

(Д. Бахтиев) Компания «Энергосеть» занимается оптимизацией энергоснабжения в нескольких регионах. Для этого нужно определить местоположение главных трансформаторных узлов, которые обеспечат минимальные потери при распределении энергии. В каждом регионе имеются несколько подрегионов, каждый из которых характеризуется тем, что расстояние от любой точки в подрегионе до точки из другого подрегиона не менее \(R\) условных единиц. Необходимо определить место для трансформаторного узла, которое находится за два шага: сначала для каждого подрегиона нужно найти его центр нагрузки — такую точку в регионе, от которой суммарное расстояние до всех остальных точек подрегиона минимально. Затем, учитывая данные о центрах нагрузки всех подрегионов, найти центральный трансформаторный узел — такая точка в одном из регионов, от которой суммарное расстояние до всех центров нагрузки минимально. Расстояние между двумя точками \((x_1, \, y_1)\) и \((x_2, \, y_2)\) на плоскости вычисляется по формуле Евклида: $$ d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$ Файл 27_A.txt содержит данные о точках двух регионов. Файл 27_B.txt содержат данные о точках трёх регионов. В первой строке каждого файла записано значения \(R.\) В каждой из следующих строк записаны координаты \(x\) и \(y\) очередной точки. Количество точек в файле 27_A.txt не превышает \(1000,\) в 27_B.txtне превышает \(10000.\)

Для каждого региона определить координаты центрального трансформаторного узла. В ответе укажите четыре целых числа. В первой строке: ближайшие целые числа значений произведения \(x\)-координаты узла на \(10000\) и \(y\)-координаты узла на \(10000\) для региона А. Во второй строке: аналогичные данные для региона В.

Файл с данными

(Л. Шастин, В. Лашин) В администрации резиденции Деда Мороза проводится активное обсуждение вопроса эффективности перевозки мириад подарков в канун волшебного Нового Года. Снегурочка настаивает на немедленном внедрении передовых технологий: «Старый мешок с письмами никуда не годится — в этой куче адресов невозможно разобраться, да и Дед уже не тот, даже таблетки не помогают. Если мы срочно не решим эту проблему, наш дорогой Дед Мороз скоро превратится в Санта Клауса! Министерство культуры РФ такое точно не одобрит». В сказочной резиденции с женщинами спорить не принято, тем более с такими молодыми и горячими, как прелестная Снегурочка. Да и аргументы в этот раз звучат убедительно...

Отдел аналитики данных возложил решение обозначенной ранее проблемы на могучие плечи СнегПрогов (снеговиков-программистов). СнегПроги предложили простую концепцию: разделить письма на группы (города) по характеристике места жительства (геопозиции) их отправителей. Благодаря этому гениальному подходу Деду Морозу не придется по сто раз перемещаться между Москвой и Владивостоком, ведь он сможет переходить к доставке подарков по Москве только после того, как развезет все подарки владивостокцам. И Декабрь, Январь и Февраль точно останутся благодарны своему хозяину. К тому же получится сэкономить на бензине, что в наше время совсем не дурно!

Одним городом СнегПроги решили считать такую группу геопозиций (точек, определенных по двум координатам \(x\) и \(y\)), в которой любая из геопозиций удалена от геопозиции из другой группы хотя бы на \(E = 20\) у.е. (условных единиц). А метрикой расстояния между двумя точками (геопозициями) уже традиционно стала формула Евклида: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$

Помогите СнегПрогам найти оптимальные геопозиции 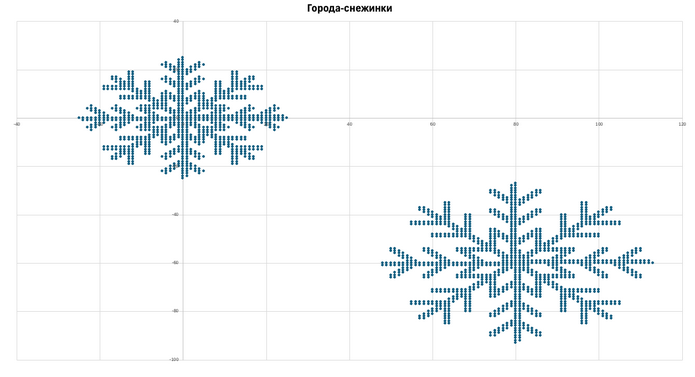в каждом городе для открытия в них новых филиалов резиденции. Лучшим местом будет считаться такая геопозиция, суммарное расстояние от которой до всех других геопозиций в этом же городе минимально. Если у вас все получится, СнегПроги получат в подарок от Деда Мороза новые чудо-компьютеры, сделанные из льдинок высочайшего качества. А вам в таком случае полагается хорошее настроение =)

В файле А хранятся записи об адресах первой партии полученных писем, образующих 2 города. В каждой строке записана информация о двух показателях геопозиции конкретного письма: сначала координата \(x,\) затем координата \(y.\) Известно, что количество записей не превышает \(2200.\) В файле Б хранятся записи об адресах второй партии полученных писем, образующих \(3\) города. Известно, что количество записей не превышает \(15~500.\) Структура хранения информации в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.

Для каждого файла определите координаты новых филиалов резиденции для всех городов, а затем вычислите два числа: \(S_x\) — среднее арифметическое абсцисс этих филиалов, и \(S_y\) — среднее арифметическое их ординат. В ответе запишите четыре числа: в первой строке сначала целую часть значения \(S_x,\) затем целую часть значения \(S_y\) для файла А, во второй строке — аналогичные данные для файла Б.

Файл с данными

(Л. Шастин) Ведущие специалисты отдела бизнес-аналитики торгового маркетплейса «Ozonyol» собирают статистику и изучают предпочтения покупателей за период летних и осенних продаж. Перед ними стоит задача — проанализировать рынок и сделать выводы об уровне спроса на товары различных категорий для выделения наиболее перспективных траекторий развития площадки с привлечением инвестиционных средств. По итогам сбора информации имеется набор данных, включающих записи о товарах, каждый из которых содержит три показателя — номер сегмента товара, характеризующий его расположение на сайте, коэффициент успешных конверсий и уровень заинтересованности поуапателей, выраженный в коэффициенте их активности. Общий спрос на товар вычисляется как среднее арифметическое второго и третьего показателей. На основании полученной информации строится графический отчёт, отражающий общий спрос на товар в зависимости от его номера сегмента, в котором записи, лежащие в области окружности с радиусом \(R\), выделяются в отдельные кластеры. В итоге решено привлекать средства на продвижение товаров только из кластеров, содержащих хотя бы \(K\) записей, причем первые вложения направить в товары-медоиды. Медоидом (центром) кластера называется такая запись о товаре, суммарное расстояние от которой до других записей в кластере минимально. Метрикой расстояния между двумя записями \(A(x_1, \, x_2)\) и \(B(x_2, \, y_2)\) является формула Евклида: $$d(A, \, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.$$ Примечание. Гарантируется, что товар принадлежит только одному из кластеров.

В файле A в первой строке записаны числа \(R\) и \(K.\) В остальных строках хранятся записи о товарах 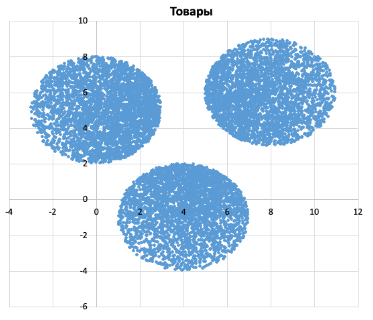за период летних продаж, образующих \(3\) кластера. В каждой строке записана информация о трёх показателях конкретного товара: сначала номер сегмента, затем коэффициент успешных конверсий и коэффициент активности. Известно, что количество записей не превышает \(1100.\) В файле Б хранятся записи о товарах за период осенних продаж, образующих \(6\) кластеров, и соответствующие осенним продажам числа \(R\) и \(K.\) Известно, что количество записей не превышает \(11~000.\) Структура хранения информации о товарах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.

Для каждого файла определите координаты медоидов (центров) всех кластеров, для продвижения которых будут привлечены инвестиционные средства, а затем вычислите два числа: \(S_x\) — среднее арифметическое абсцисс центров кластеров, и \(S_y\) — среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(S_x \times 100~000,\) затем целую часть произведения \(S_y \times 100~000\) для файла А, во второй строке — аналогичные данные для файла Б.

Файл с данными