Информатика. ЕГЭ
Задания для подготовки
Задачи разных лет из реальных экзаменов, демо-вариантов, сборников задач и других источников
Задачи разных лет из реальных экзаменов, демо-вариантов, сборников задач и других источников
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. 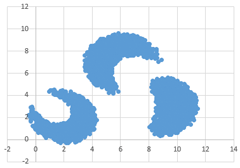 В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров.  В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров.  В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком. Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба. 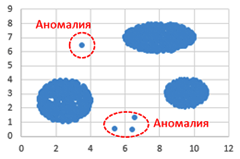 Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба.  Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба.  Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Кластер звёзд – это набор звёзд (точек) на графике. Каждая звезда обязательно принадлежит только одному из кластеров. Центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Расстояние между двумя точками \(A(x_1, \, y_1)\) и \(B(x_2, \, y_2)\) вычисляется по формуле:
$$
d(A, \, B) = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}
$$
Аномалиями назовём точки, находящиеся на расстоянии более одной условной единицы от точек кластеров. При расчётах аномалии учитывать не нужно. Даны два входных файла (файл A и файл Б). В файле A хранятся данные о звёздах двух кластеров. В каждой строке записана информация о расположении на карте одной звезды: сначала координата \(x\), затем координата \(y\) (в условных единицах). Известно, что количество звёзд не превышает \(1000\). В файле Б хранятся данные о звёздах трёх кластеров. Известно, что количество звёзд не превышает \(10~000\). Структура хранения информации о звездах в файле Б аналогична файлу А. Возможные данные одного из файлов иллюстрированы графиком.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: \(P_x\) – среднее арифметическое абсцисс центров кластеров, и \(P_y\) – среднее арифметическое ординат центров кластеров. В ответе запишите четыре числа: в первой строке сначала целую часть произведения \(P_x \times 100~000\), затем целую часть произведения \(P_y \times 100~000\) для файла А, во второй строке – аналогичные данные для файла Б.